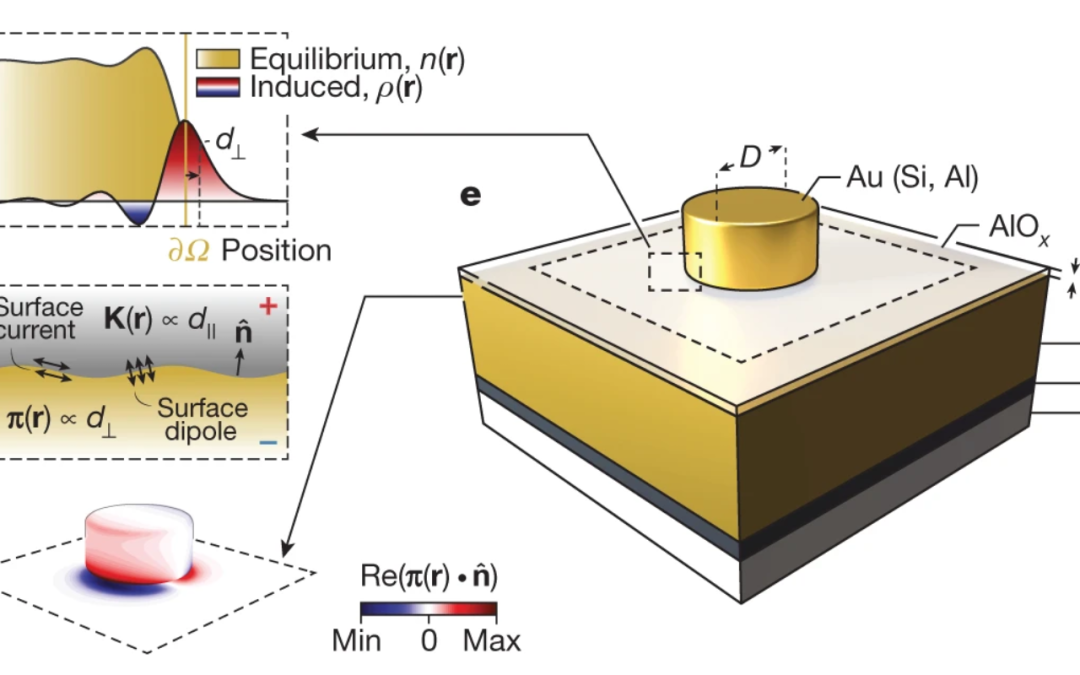
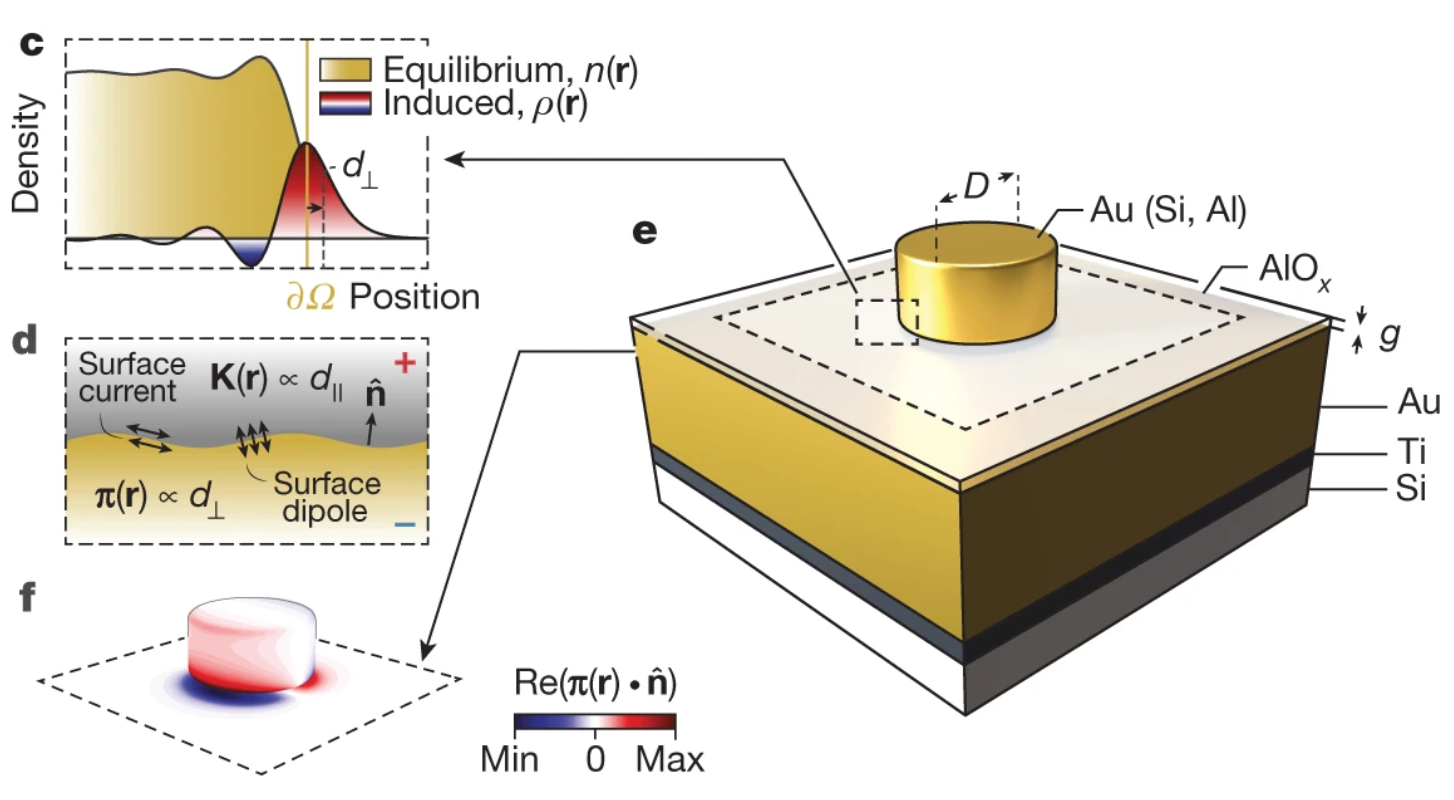
The macroscopic electromagnetic boundary conditions, which have been established for over a century, are essential for the understanding of photonics at macroscopic length scales. Even state-of-the-art nanoplasmonic studies, exemplars of extremely interface-localized fields, rely on their validity. This classical description, however, neglects the intrinsic electronic length scales (of the order of ångström) associated with interfaces, leading to considerable discrepancies between classical predictions and experimental observations in systems with deeply nanoscale feature sizes, which are typically evident below about 10 to 20 nanometres. The onset of these discrepancies has a mesoscopic character: it lies between the granular microscopic (electronic-scale) and continuous macroscopic (wavelength-scale) domains. Existing top-down phenomenological approaches deal only with individual aspects of these omissions, such as nonlocality and local-response spill-out. Alternatively, bottom-up first-principles approaches—for example, time-dependent density functional theory are severely constrained by computational demands and thus become impractical for multiscale problems. Consequently, a general and unified framework for nanoscale electromagnetism remains absent. Here we introduce and experimentally demonstrate such a framework—amenable to both analytics and numerics, and applicable to multiscale problems—that reintroduces the electronic length scale via surface-response functions known as Feibelman d parameters. We establish an experimental procedure to measure these complex dispersive surface-response functions, using quasi-normal-mode perturbation theory and observations of pronounced nonclassical effects. We observe nonclassical spectral shifts in excess of 30 per cent and the breakdown of Kreibig-like broadening in a quintessential multiscale architecture: film-coupled nanoresonators, with feature sizes comparable to both the wavelength and the electronic length scale. Our results provide a general framework for modeling and understanding nanoscale (that is, all relevant length scales above about 1 nanometre) electromagnetic phenomena.
A complete description of the work may be found here.